As the second installment in this series of posts, I will touch upon on the topic of privacy in data science and algorithms. In particular, I’m going to discuss a relatively novel concept of privacy called differential privacy that promises, similar to algorithmic fairness, a way of quantifying the privacy of AI algorithms.
When we, as humans, talk about privacy, we mostly refer to a desire to not be observed by others. However, what does privacy mean in the context of algorithms that “observe” us by using data that has information on us?
What do we mean by “privacy” in the context of statistics and machine learning?
In a very general sense, we could say that privacy will be preserved if, after analysis, the algorithm that used our data (e.g. an application on our smartphones) doesn’t know anything about us. We want our machine learning models to only learn what they’re supposed to learn from data and nothing more — without retaining any information on particular individuals in the dataset.
This request was addressed in the proposition of an ad omnia guarantee of privacy in 1977 by Tor Dalenius. The proposition was then discussed by Cynthia Dwork, pioneer of differential privacy, in her paper from 2008:
Anything that can be learned about a respondent from the statistical database should be learnable without access to the database.
This essentially means that we should make sure that everything that a model learns about an individual is already public information. However, this is difficult to implement in statistical analysis for several reasons. First, how do we know what information is publicly available? Second, how do we selectively access any private dataset for that matter, especially in cases where the application needs certain information relevant for its purpose (for example, a model that determines whether a person suffers from some disease)?
Differential privacy to the rescue
With those issues in mind, differential privacy has been developed to enable statistical analyses on datasets without compromising the privacy of individuals whose records may be contained in the dataset. As with algorithmic fairness, the ideas behind differential privacy stem from the application of algorithmic concepts to the study of privacy.
In her intuitive definition of differential privacy in The Algorithmic Foundations of Differential Privacy, Cynthia Dwork mentions its fundamental motivation:
“Differential privacy” describes a promise, made by a data holder, or curator, to a data subject: “You will not be affected, adversely or otherwise, by allowing your data to be used in any study or analysis, no matter what other studies, data sets, or information sources, are available.”
The last part holds one of the key ideas behind differential privacy: it aims to protect an individual’s private information regardless of whatever other information might be available to a potential attacker (perhaps in other datasets, for example).
Why don’t we just anonymise data?
You might be wondering: Can’t we simply anonymise data? It turns out that anonymisation precisely cannot guarantee this last bit of Cynthia Dwork’s promise: that the users are protected against attacks in case there are other information sources out there.
One of the most known examples of this flaw of anonymisation of data is the Netflix Prize dataset, a large dataset of users’ movie reviews which Netflix released that contained names of movies and individuals replaced by integers. Researchers A. Narayanan and V. Shmatikov showed in their paper Robust De-anonymization of Large Sparse Datasets that, even without releasing private information about users, it was still possible to uncover private aspects of the information by using another private dataset that was independently released and anonymised. In this case, Narayanan and Shmatikov used the IMDB movie site to find individuals who rated movies both on Netflix and IMDB; they ultimately were able to de-anonymise 99% of both the names of the movies and users.
This research is just one example of how data anonymisation can be a fundamentally flawed technique with a weak promise of privacy. If an attacker has auxiliary information from other data sources, something we can’t ever really know or guarantee protection against, anonymisation is not enough. Differential privacy strengthens the promise of privacy as it protects users’ privacy even against attackers that use other datasets.
Intuition behind differential privacy
The math that differential privacy is based on was developed years ago, and differential privacy relies on it to give a rigorous mathematical definition of privacy. Essentially, differential privacy promises that an algorithm is (differentially) private if, by looking at the output, an observer cannot tell whether any individual’s data is included in the dataset used to produce said output.
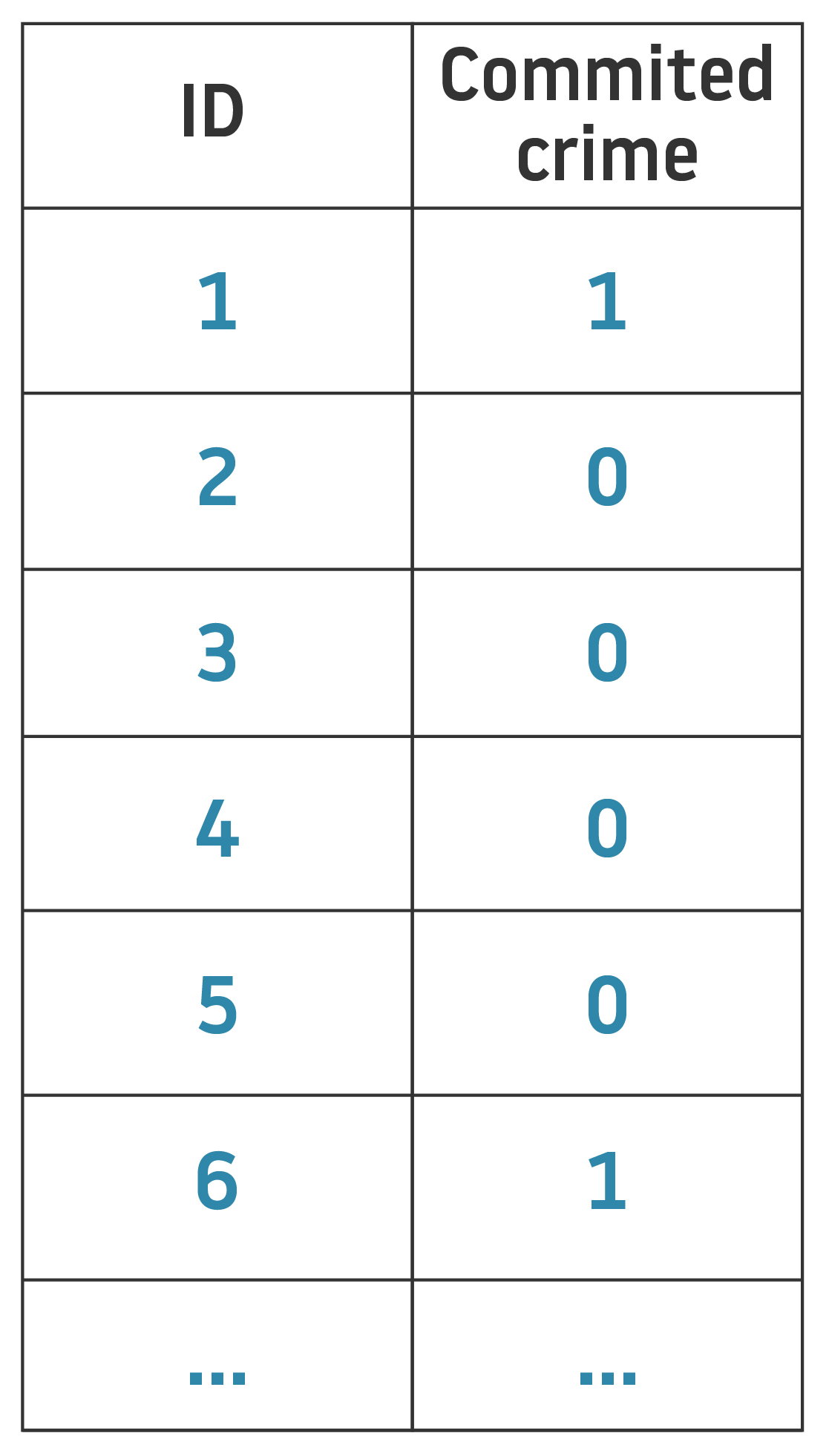
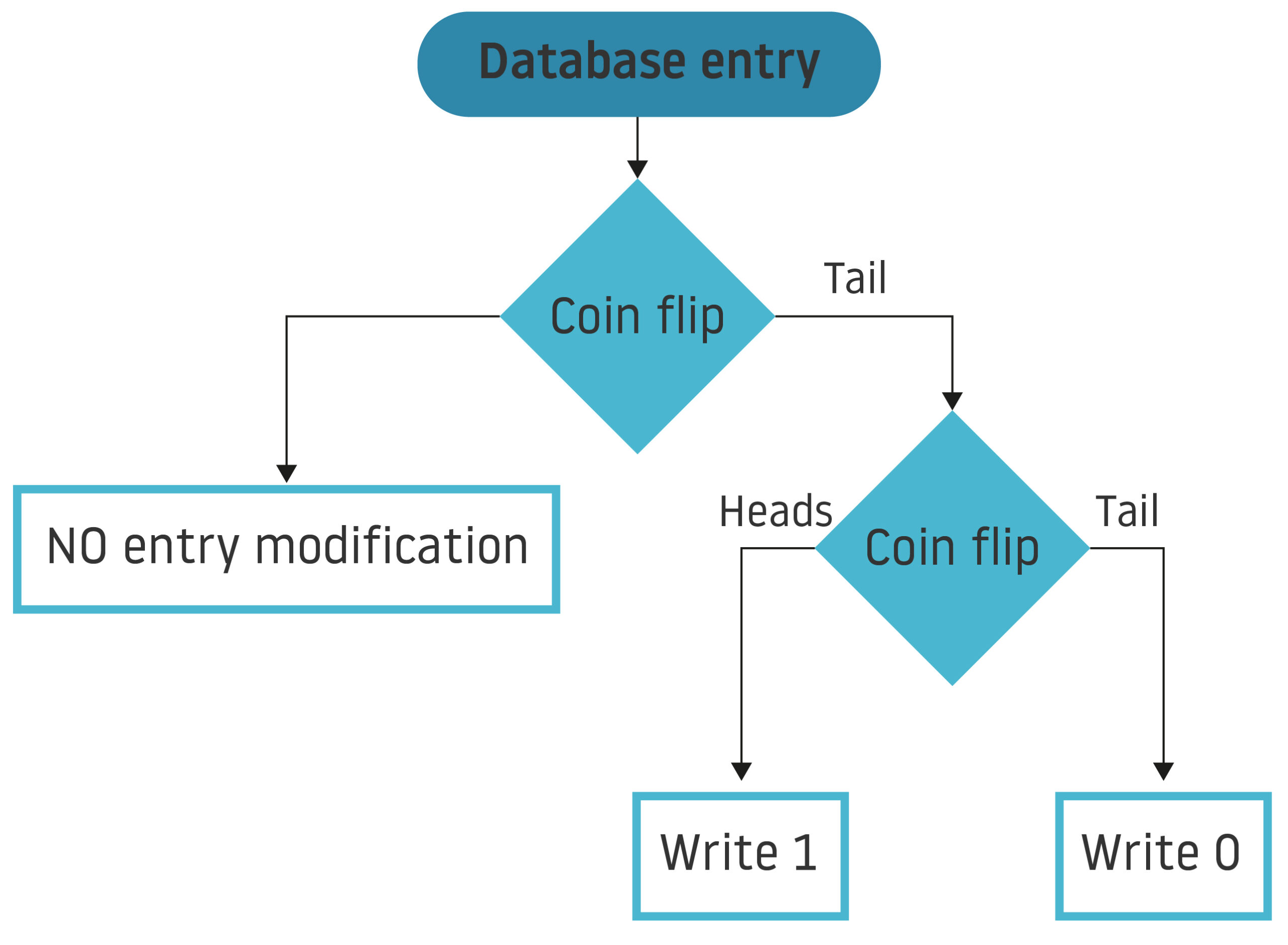
To better understand the fundamental concept of differential privacy, let’s look at an example of a simple database with only one column: user responses to a question (e.g. Have you ever committed a crime?), with 1 being a YES and 0 a NO (in addition to the ID column).