Graphs are everywhere. Many of us use them or come across them daily. In its essence, a graph is an abstract data type that requires two basic building blocks: nodes and vertices. A graph utilises the basic idea of using vertices to establish relationships between pairs of nodes. In terms of applications, many real world relationships are best modeled using graph structures. A social network such as Facebook, a virus spreading during an epidemic outbreak, a highway system connecting different cities, and molecule representations are just a few examples of real world structures often modeled with graphs. Graphs are omnipresent in aviation research as well: a graph of airports and flights connecting them, flights and connecting passengers, airlines forming alliances, etc.

What makes the graph representation so powerful?

The origins of graph theory date back to the 18th century and the mathematician named Leonhard Euler. In 1735, he solved the problem known today as Seven Bridges of Königsberg. Back then, Königsberg was a city in Prussia divided into four bodies of land by the river Pregel. Seven bridges connected those separate bodies of land, posing a specific question to Euler: was it possible to walk around the city, ending back at the starting point and crossing each of the seven bridges exactly once? Euler proved not. What is more influential is that, in order to do so, he used a graph representation, laying the foundations of studying graphs as mathematical structures and modelling real world problems with graphs.

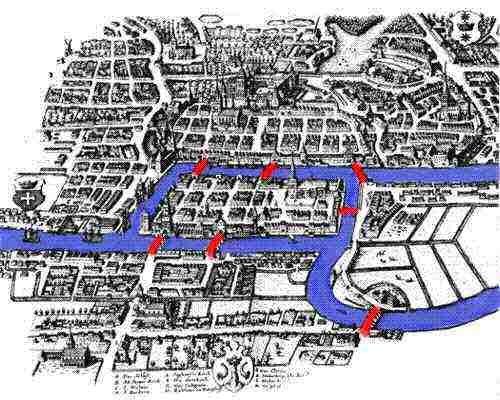
Nevertheless, the potentially interesting patterns could still be there, hidden in that massive data representation, even though humans cannot spot them. The following question naturally arises: if humans have benefited so much from utilising graph structures, could intelligent algorithms benefit from them as well?  We might not be able to inspect massive graphs and easily extract useful knowledge from them, but machines might be able to.

What’s in it for machine learning?

Imagine you have a data set full of graph structured data. Ideally, we want to utilise that data structure and build functions that operate over graphs. In many applications, treating the underlying data as a graph can achieve greater efficiency. While machine learning is not tied to any particular representation of data, most machine learning algorithms today operate over real number vectors. Therefore, applying machine learning techniques to graphs can be a challenging task. In a way, as humans have difficulties with perceiving huge graphs, so do computers. It is challenging to efficiently store a large graph in a tensor and to feed it to an algorithm.

Furthermore, many neural networks operate on structured data. For example, Recurrent Neural Networks for text mining operate on sequences of words. Essentially, sentences can be seen as chains of nodes (words), a special type of graph with a very clearly defined topology. However, in general, graphs have arbitrary topologies. Often it is impossible to define the beginning of a graph. Or, there is no clear best scheme on how to traverse it.

In order to feed graph data into a machine algorithm pipeline, so-called embedding frameworks are commonly used. They basically perform a mapping between each node or edge of a graph to a vector. A large number of frameworks has been designed so far that intend to encode graph information into low-dimensional real number vectors of fixed length. One embedding framework that gained a lot on popularity since its inception is node2vec, a method that learns features for networks by exploring nodes neighbourhoods through random walks.

Graphs powering artificial intelligence

Graph embeddings are just one of the heavily researched concepts when it comes to the field of graph-based machine learning. The research in that field has exploded in the past few years. One technique gaining a lot of attention recently is graph neural network. The idea of graph neural networks has been around since 2005, stemming from a paper by Gori et al. Since then, different graph network models have been explored, until in 2017, Gilmer et al. provided a unification of by then developed methods, causing an avalanche of research papers.

In 2018, a positional paper on graph networks, titled Relational inductive biases, deep learning, and graph networks, and published by a group of researchers from DeepMind, GoogleBrain, MIT and University of Edinburgh, sparked many interesting discussions in the artificial intelligence community. The paper argues that graph networks could perform relational reasoning and combinatorial generalisation – two capabilities that, according to the authors’ argument, need to be prioritised if we want AI to achieve human-like performance. Reading what look like promises of being close to finding the master algorithm in AI understandably raised a lot of commotion. In any case, it is a testament to the field of graph-powered machine learning going viral in the research community and buzzing with possibilities.

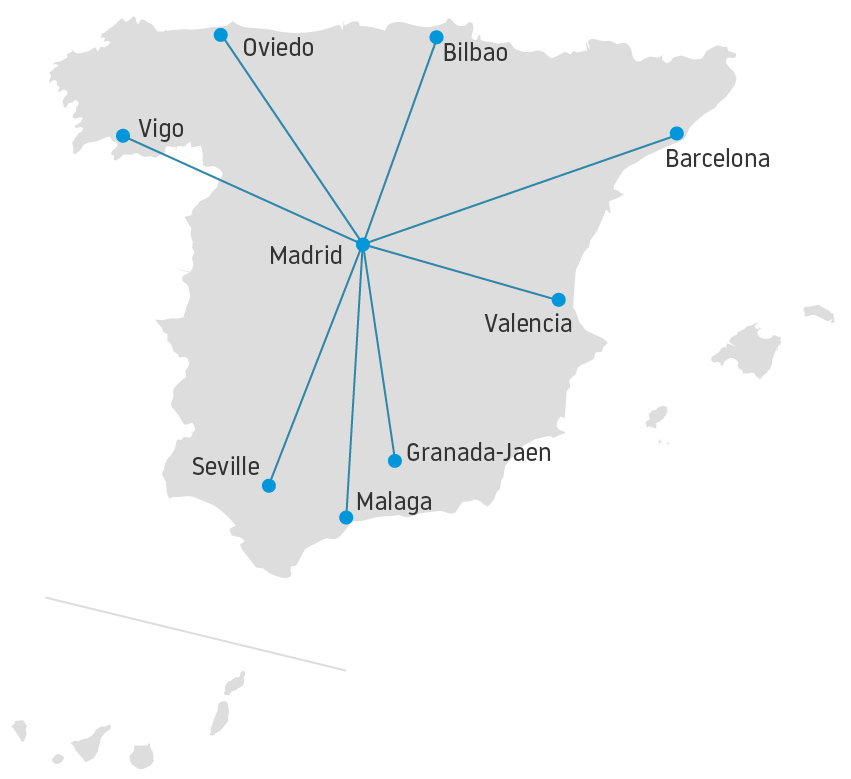
Finally, as I have mentioned, aviation and air traffic management are fields that are very familiar with graph representations. In air transport, very complex networks are often analysed to derive conclusions about the robustness of the system, its resilience or to try to detect emerging behaviour. Moreover, air transport networks can be very complex due to its size, topologies, characteristics, etc. With data science in aviation finally taking off, we could profit a lot by paying attention to the advances being made in graph-based artificial intelligence research.

I hope this teaser post has whetted your appetite for graphs in machine learning. If so, then stay tuned for more detailed posts about it in the future. Without repeating myself too much, if the saying is that a picture speaks a thousand words, it will be surely interesting to see what graph structures will be able to say to machine learning algorithms.