Haversine distance: Why you should not go straight to the point
Ernesto Gregori
“The shortest distance between two points is a straight line” is a phrase that we have all heard in high school—but it’s not always true.
In a Euclidean space, straight lines are the shortest distances when considering basic distance, or Euclidean distance. But what about other spaces?
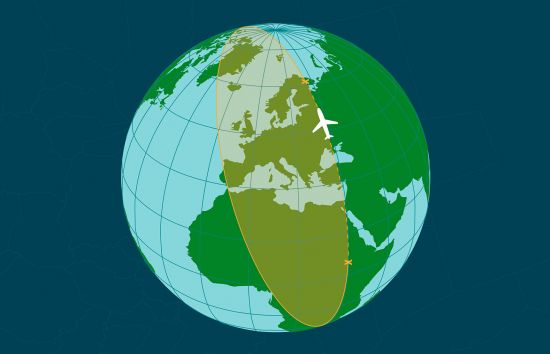
Let’s take the case of an aircraft trajectory: two points on the surface of the Earth can be connected with a straight line to minimise distance, but since an aircraft has to fly over the Earth and not through it, this distance does not give much information. To solve this problem, we can introduce the great-circle distance, also known as the Haversine distance. This formula computes the distance by replacing a straight line with a circle on the sphere connecting the two points, where the center coincides with the center of the sphere, and then computing the length of the shortest arc.
When checking the route of a plane, the curved trajectory is a geodesic, or the generalization of straight lines in curved spaces. But if seen on a map, those trajectories don’t look like circles either, since they are deformed. This is a side effect of the projection of the Earth onto a map: we cannot preserve all the information contained in a 3D space, like the Earth, and display it onto a flat 2D map without having to take some assumptions and losing generality. Therefore, we alter the original distribution, resulting in the geodesic not being represented as a circle (for that projection).
There are in fact many map projections, such as Mercator or Cassini, and each of them has advantages and disadvantages (we may need maps that preserve areas, distances along meridians or any other feature). Each of those projections will show the same geodesic in a different way, depending on their design.
However, for small distances, the length of the geodesic is almost the same as the length of a straight line. Therefore, it is possible to approximate it with the distance that we are all familiar with. This is useful for computing short distances, since using the Euclidean approach involves fewer calculations, though it is less accurate. This trade-off between accuracy and computational expense suggests that, for short distances, we have the choice between slightly worse results with fewer calculations, or better results with more calculations.


